递归的思想

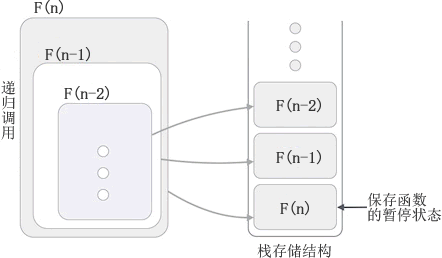
基本思想：某个函数直接或间接调用自身的方法

哈！自己调自己！

套路：递归三部曲！

某个函数直接或间接的调用自己，递归实质上是函数的嵌套执行，因此首先要确定函数的参数和返回值。

由于不断调用自身，因此一定要把握住出口，否则会出现栈溢出或者死循环。因此需要确定递归的结束条件。

递归是函数的嵌套执行，那么单层递归到底执行了什么逻辑---单层递归的逻辑。

记住递归的三部曲

参数和返回值
递归的结束条件
单层递归的逻辑（递归调用出现在这里）

例子：

计算斐波那契数列

数列：1 1 2 3 5 8 13 ...

前一个数由前两个数相加得到，这里就存在了递归思想。

设计一个递归函数：

参数为第n个位置的斐波那契额数，返回值为该位置的斐波那契数
结束条件：当第n个位置的前面的数小于2时，无法继续递归。前两个数分别为1 1
单层递归的逻辑：第n个数等于第n-1个数 + 第n-2个数

int f(int n){
        // 递归终止条件 0返回0,1返回1
        if (n <= 1){
            return n;
        }
        // 单层递归逻辑
        int r = f(n - 1) + f(n - 2);
        // 递归返回值
        return r;
    }

例子：

计算二叉树的最大深度---或计算二叉树根节点的高度

https://leetcode.cn/problems/maximum-depth-of-binary-tree/

没一个节点的高度，等于该节点的左右子树的高度最大值 + 1，这里存在了递归思想，因此可以使用递归解决。

设计一个递归函数：

参数是节点，返回值是该节点的高度
结束条件：当该节点为空时，不再进入递归，且高度是0
单层递归的逻辑：节点的高度等于左右子节点的高度最大值+1

class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null) return 0;
        return depth(root);
    }
    // 递归参数
    int depth(TreeNode root){
        // 递归结束结束条件
        if(root == null){
            return 0;
        }
        // 单层递归逻辑：左右子树高度最大值+1
        int h1 = depth(root.left);
        int h2 = depth(root.right);
        // 递归返回值
        return Math.max(h1,h2) + 1;
    }
}

例子：

对称二叉树

https://leetcode.cn/problems/symmetric-tree/description/

判断一个节点root是否是对称二叉树，看该节点root的两个子树left right是否对称。

判断left right是否对称，即判断left的左节点是否right的右节点对称，left的右节点是否和right的左节点对称。此时进入了判断子树是否对称的逻辑，即可使用递归。

设计一个函数：

参数是节点，返回值是boolean
结束条件：当存在不对称的情况，立即停止递归，返回false
单层递归逻辑：判断左右子树的子节点是否对称

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */

//  注意：对称可不是检查每个子树的节点是否对称，而是一个节点，他的左右孩子是否对称。
// 判断一个节点是否对称，即判断它的左右孩子是否对称，即判断
// ● 左孩子的左孩子，是否等于右孩子的右孩子
// ● 左孩子的右孩子，是否等于右孩子的左孩子
// 即：
// 判断left是否和right对称
// ● 条件1：判断left的左孩子和right的右孩子是否对称
//   ○ 进入递归
// ● 条件2：判断left的右孩子和right的左孩子是否对称
//   ○ 进入递归
// ● 当条件1、2都成立，说明left和right对称
class Solution {
    public boolean isSymmetric(TreeNode root) {
        return compare(root.left,root.right);
    }
    // 判断两个子树是否对称
    // 递归参数：左右子树的根节点
    boolean compare(TreeNode left,TreeNode right){
        // 递归结束条件
        if(left == null && right == null){
            return true;
        }else if(left == null && right != null){
            return false;
        }else if(left != null && right == null){
            return false;
        }else if(left.val != right.val){
            return false;
        }
        // 单层递归的逻辑：递归判断left right的子节点是否对称
        boolean outer = compare(left.left,right.right);
        boolean inner = compare(left.right,right.left);
        // 递归返回值
        return outer && inner;
    }
}